Математические формулы в лотерее являются частью теории вероятностей и комбинаторной математики.

Что же мы подразумеваем под этим интуитивным понятием вероятности? С точки зрения математики возможны две различные интерпретации этого сугубо абстрактного понятия. В первой из них понятие вероятности ассоциируется с частотой появления данного события в серии опытов, в каждом из которых анализируемое событие может появиться или не появиться. Такое событие математики называют случайным.
 

Как вычислить вероятность?

Существует так называемый закон больших чисел, справедливость которого доказывается в теории вероятностей. Согласно этому закону, в любой серии опытов при увеличении их числа, частота появления случайного события всегда стабильно стремится к одной и той же величине и это предельное значение можно принять за вероятность Р(А) (probability — на английском языке):
 
 
Таким образом, согласно этому утверждению, чтобы найти вероятность события, нужно провести достаточно длинную серию опытов и полученную частоту выразить в процентах.

А нельзя ли определить вероятность выигрыша априори, то есть до начала опытов? Оказывается, что в ряде случаев это возможно. Метод, который используется для априорного определения величин вероятности, основан на втором возможном варианте ее интерпретации и состоит он в следующем:

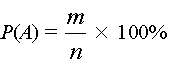
то — есть вероятность появления события А равна отношению числа m — благоприятных событий для А к полному числу n — возможных элементарных событий, выраженному в процентах.

Рассмотрим теперь задачу, более близкую к нашим интересам. А эти интересы в данном случае связаны с подсчетом вероятностей угадывания цифр в розыгрышах Лото 6/49. По правилам этой игры, требуется угадать шесть отобранных (счастливых) номеров из общего количества имеющихся в наличии сорока девяти. Для наглядности заштрихуем «счастливые номера», как это показано на рисунке.

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49

Какова вероятность того, что перевернутый номер окажется заштрихованным? Очевидно, она и в этом случае равна отношению числа благоприятных для нас исходов (заштрихованных номеров, а их число равно 6) к полному числу всех возможных исходов (то есть полному числу номеров, число которых 49). Таким образом, вероятность угадать одну из шести отобранных номеров равна 6/49, а вероятность не угадать, соответственно — 43/49.

Если сложить теперь вероятности этих двух возможных исходов, то, как и следовало ожидать, сумма всех вероятностей окажется равной 1. Конечно, хоть что-нибудь, но должно же случиться с достоверностью (то есть с вероятностью 100%). Как говорят, уж если не выиграю, то проиграю.

При второй попытки полное число оставшихся номеров, уже становится равным 48 (один номер уже был разыгран в первом туре). Таким образом, для всех возможных вариантов исхода получаем:

• Если в первом туре был угадан заштрихованный номер:
  Вероятность угадать заштрихованный номер становится равно 5/48, а вероятность выпадения незаштрихованного номера составит 43/48.
• Если в первом туре был угадан незаштрихованный номер:
  Вероятность угадать заштрихованный номер становится равно 6/48, а вероятность выпадения незаштрихованного номера составит 42/48.

Таким образом, при двух подходах жеребьевки возможны четыре варианта результата (первый подход + второй подход):

1) угадал + не угадал: p = 6/49 x 43/48 = 0,1097

2) не угадал + угадал: p = 43/49 x 6/48 = 0,1097

3) угадал + угадал: p = 6/49 x 5/48 = 0,0128

4) не угадал + не угадал: p = 43/49 x 42/48 = 0,7679

Нетрудно убедиться, что и в этом случае сумма вероятностей равна 1.
 

 

Как вычислить количество всех возможных результатов?

Легко заметить, что по мере увеличения количества подходов общее количество возможных вариантов результата увеличивается очень быстро, а именно: общее количество возможных вариантов результата для n подходов розыгрышей равно 2ⁿ (2 в степени n).

Например, при трех подходах у нас уже будет 2³ = 8 возможных вариантов результата:

1) угадал + угадал + угадал: вероятность = 0,0011

2) угадал + угадал + не угадал: вероятность = 0,0117

3) угадал + не угадал + угадал: вероятность = 0,0117

4) не угадал + угадал + угадал: вероятность = 0,0117

5) угадал + не угадал + не угадал: вероятность = 0,0980

6) не угадал + угадал + не угадал: вероятность = 0,0980

7) не угадал + не угадал + угадал: вероятность = 0,0980

8) не угадал + не угадал + не угадал: вероятность = 0,6698
 

Как вычислить количество комбинаций?

Зная общее количество возможных вариантов, давайте теперь выясним, сколько из этих вариантов содержат угаданные числа. Количество этих вариантов на самом деле является количеством всех возможных комбинаций угаданных заштрихованных чисел.

Предположим, что мы отметили шесть произвольных чисел и хотим узнать, сколько существует вариантов, в которых будет угадано 4 цифры из 6. Число способов, которыми можно угадать 4 из этих 6 номеров, математики называют числом сочетаний и обозначают его . Эта запись читается так: «число сочетаний из шести по четыре».

Предположим, что угаданы числа 12, 14, 30 и 36. Сколько вариантов существует для такого угадывания? Число 12 может быть угадано в любой из 6 попыток, то-есть может быть названо 1-м, 2-м, 3-м, 4-м, 5-м или 6-м. Следовательно, для угадывания числа 12 существует 6 различных вариантов. Второе число 14 может быть угадано в любой из оставшихся пяти попытках, следовательно, для его угадывания имеется 5 различных вариантов. Продолжая эти рассуждения, легко прийти к выводу, что для угадывания числа 30 существует 4 различных варианта, а числа 36 — 3 варианта. Следовательно, для угадывания четверки чисел из шести «счастливых» существуют всего 6х5х4х3 вариантов.

Но не все эти варианты различны. Предположим, что эти числа были угаданы в первых же четырех попытках. Тогда все эти варианты, соответствующие различной последовательности заполнения «счастливых» номеров в тех же самых попытках (всего 24 варианта), фактически представляют 1 вариант (число перестановок 4 элементов равно 4х3х2х1=24).

Окончательно для искомого числа сочетаний мы получили формулу:
 
 
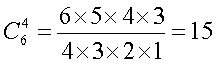
Эта формула для числа сочетаний является справедливой и при любых других количествах отмеченных чисел и количествах «угаданных». В общем случае можно сформулировать следующее правило: для того, чтобы определить количество возможных вариантов с m угаданными числами для отмеченных n чисел, необходимо вычислить число сочетаний:
 
 
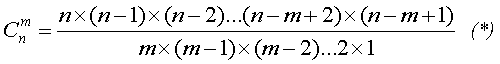
В этой формуле число сомножителей в числителе и знаменателе одинаково и равно m.

Также по этой формуле рассчитывается общее количество возможных комбинаций для игр в лотереи. А для Лото 6 из 49 получаем:
 
 
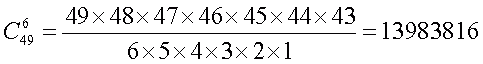
На основе формулы (*) заполняется таблица с количеством выигрышей для каждой категории выигрышей, в зависимости от того, сколько чисел было отмечено и сколько чисел было угадано. См. В качестве примера таблицу для Лото 6/49.
 

 

Средний выигрыш одной комбинации

Теперь перейдем к оценке выигрышей, которые рассчитываются на основе среднего выигрыша одного игрового варианта, разыгранного для каждой призовой категории. Средний выигрыш представляет собой вероятность возникновения этого выигрыша, умноженную на общую сумму денег, предложенную для данной призовой категории.

Согласно математическим расчетам, средние значения выигрыша для каждого рубля, потраченного в простой игровой системе и в развернутой игровой системе, одинаковы, независимо от того, сколько чисел было отмечено. Но все же различие между этими двумя игровыми системами существует.

Если мы возьмем статистическую характеристику для большого количества участников игры, то заметим, что при увеличении количества отмеченных чисел в билете в целом, выигрыши становятся крупнее, но вероятность более мелких выигрышей при этом резко уменьшается. Отсюда можно сделать вывод, что если вы стремитесь только к крупному выигрышу, то для вас предпочтительнее будет развернутая система игры, но если не любите сильно рисковать и считаете, что лучше иметь «синицу в руках, чем журавля в небе», то лучше подойдет простая система игры.
 

Вероятность последовательных неудач

Какова вероятность длинной серии неудач, если ставить в каждом туре на одну и ту же комбинацию? Существует формула, которая называется формулой Бернулли. Она позволяет найти вероятность того, что в результате участия в n турах игры количество туров без единого выигрыша будет равно m:
 
 
где q определяет вероятность «несчастного» случая только для одного тура т.е. не были угаданы 6, 5 и 4 номеров и определяется формулой:
 
 
где , и вероятности угадывания 4-х, 5-ти и 6-ти чисел соответственно.

Для примера, на основе формулы Бернулли и некоторых исходных статистических данных были получены следующие результаты вероятностей неудач для 4 розыгрышей:

1) Не было ни одного выигрыша: m = 4, P = 0,02 (2%)

2) Был один выигрыш: m = 3, P = 0,13 (13%)

3) Было два выигрыша: m = 2, P = 0,33 (33%)

4) Было три выигрыша: m = 1, P = 0,37 (37%)

5) Все туры были выигрышными: m = 0, P = 0,15 (15%)

2% + 13% + 33% + 37% + 15% = 100%

Как видим, вероятность последовательных проигрышей с одной и той же комбинацией чисел уменьшается с увеличением количества участий, но появление выигрыша не гарантирует того, что он будет большим.

И все-таки, несмотря на то, что непредсказуемость результатов азартной игры является ее основной чертой, нельзя ли избрать какую-то оптимальную стратегию? Единственный совет, который можно дать в этом случае — это рационально выбрать определенную систему игры и последовательно придерживаться её.