Formulele matematice la loto fac parte din teoria probabilității și matematica combinatorică.

Ce înțelegem prin această noțiune intuitivă de probabilitate? Din punctul de vedere al matematicii, o interpretare a acestui concept, pur abstract, constă în asocierea lui cu frecvența de apariție a unui eveniment într-o serie de experimente, în care evenimentul analizat poate apărea sau nu. Un astfel de eveniment matematicienii îl numesc eveniment aleatoriu.
 

Cum se calculează probabilitatea?

Există o lege care a fost demonstrată în teoria probabilității, care se numește legea numerelor mari, conform căreia, în orice serie de experimente cu creșterea numărului de experimente, frecvența de apariție f(A) a evenimentelor aleatorii întotdeauna în mod constant tinde către una și aceeași mărime, valoarea limită a căreia poate fi luată ca probabilitatea P(A) (probability – din limba engleză):
 
 
Astfel, conform acestei afirmații, pentru a găsi probabilitatea unui eveniment, trebuie să efectuăm o serie suficient de lungă de experimente, iar frecvența de apariție obținută de exprimat ca procent.

Dar este oare posibil să determinăm a priori probabilitatea de câștig, adică înainte de începerea experimentelor? Da, în unele cazuri este posibil. Metoda utilizată pentru determinarea a priori a valorilor de probabilitate, se bazează pe a doua versiune posibilă de interpretare a concepției de probabilitate: 

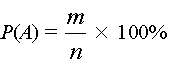
unde n este numărul total de evenimente elementare posibile, iar m este numărul de evenimente favorabile A. Adică, probabilitatea evenimentului A este egal cu raportul dintre numărul de evoluții favorabile pentru A la numărul total de evenimente elementare posibile, exprimat în procent.

Să analizăm acum problema care este mult mai apropiată de interesele noastre și anume calcularea probabilităților de ghicire a numerelor la tragerile loto. În continuare vom lua ca exemplu jocul loto 6/49. Conform regulilor acestui joc este necesar de ghicit șase numere extrase (norocoase) din numărul total de patruzeci și nouă de numere disponibile.

Vom reprezenta schematic toate numerele la loto 6/49, iar “numerele norocoase” le vom hașura, așa cum se arată în desen. 

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49

Care este probabilitatea că se va extrage un număr hașurat? Evident că și în acest caz, probabilitatea va fi egală cu raportul dintre numărul de rezultate favorabile pentru noi (6 cifre hașurate) la numărul total de rezultate posibile (adică la numărul total de cifre care este egal cu 49). Astfel, probabilitatea de a ghici un număr din cele șase numere hașurate este egală cu 6/49, iar probabilitatea de a nu ghici aceste numere este egală cu 43/49.

Dacă să adunăm acum probabilitățile acestor două desfășurări posibile pentru prima rundă de extragere, apoi cum și era de așteptat, suma lor este egală cu 1. Cum se zice, 100% ceva se va întâmpla, ori numărul „va fi ghicit” ori „nu va fi ghicit”.

Pentru a doua rundă de extragere vor rămâne doar 48 de numere în joc (un număr deja a fost extras în prima rundă). Astfel pentru toate variantele posibile de desfășurare obținem:

• Dacă în prima rundă a fost ghicit un număr hașurat:
  Probabilitatea de a ghici un număr hașurat devine egală cu 5/48, iar de a extrage un număr nehașurat, egală cu 43/48.
• Dacă în prima rundă a fost extras un număr nehașurat:
  Probabilitatea de a ghici un număr hașurat devine egală cu 6/48, iar de a extrage un număr nehașurat, egală cu 42/48.

Astfel, pentru două runde de extragere avem patru variante de rezultate posibile (prima rundă + a doua rundă):

1) ghicit + neghicit: p = 6/49 x 43/48 = 0,1097

2) neghicit + ghicit: p = 43/49 x 6/48 = 0,1097

3) ghicit + ghicit: p = 6/49 x 5/48 = 0,0128

4) neghicit + neghicit: p = 43/49 x 42/48 = 0,7679

Și iar, dacă adunăm toate aceste probabilități vom obține 1. Fiindcă toate aceste variante posibile de desfășurare, împreună reprezintă 100% certitudine completă.
 

 

Cum se calculează numărul total de rezultate posibile?

Observăm, că odată cu mărirea numărului de runde crește foarte rapid și numărul total de variante de rezultate posibile, iar mai exact: Numărul total de variante de rezultate posibile pentru n runde de extrageri este egal cu 2ⁿ (2 la puterea n).

De exemplu, pentru 3 runde vom avea deja 2³ = 8 variante de rezultate posibile:

1) ghicit + ghicit + ghicit: probabilitatea = 0,0011

2) ghicit + ghicit + neghicit: probabilitatea = 0,0117

3) ghicit + neghicit + ghicit: probabilitatea = 0,0117

4) neghicit + ghicit + ghicit: probabilitatea = 0,0117

5) ghicit + neghicit + neghicit: probabilitatea = 0,0980

6) neghicit + ghicit + neghicit: probabilitatea = 0,0980

7) neghicit + neghicit + ghicit: probabilitatea = 0,0980

8) neghicit + neghicit + neghicit: probabilitatea = 0,6698
 

Cum se calculează numărul de combinații?

Știind numărul total de variate posibile să aflăm acum câte din aceste variante conțin numerele hașurate ghicite. Numărul acestor variante este de fapt numărul de combinări posibile ale numerelor hașurate care au fost ghicite.

Să presupunem că din 6 numere hașurate au fost ghicite doar 4. Numărul de posibilități cu care puteți ghici 4 din 6 numere matematicienii îl numesc numărul de combinări și îl notează ca . Această expresie se citește astfel: „Numărul combinărilor de șase luate câte patru”.

Să presupunem că am ghicit numerele hașurate 12, 14, 30 și 36. Câte variante există pentru o astfel de ghicire? Numărul 12 poate fi ghicit în oricare dintre cele 6 încercări (o extragere completă), adică poate fi extras primul, al 2-lea, al 3-lea, al 4-lea, al 5-lea sau al 6-lea. Prin urmare, există 6 posibilități diferite pentru a ghici numărul 12. Al doilea număr 14 poate fi ghicit în oricare dintre cele cinci încercări rămase, prin urmare există 5 variante diferite pentru a-l ghici. Continuând astfel, ajungem la concluzia că există 4 variante diferite pentru a ghici numărul 30 și numărul 36 are 3 variante. Prin urmare, există doar 6x5x4x3 de variante pentru a ghici cele 4 din cele 6 numere „norocoase” hașurate.

Dar nu toate aceste variante posibile sunt diferite între ele. Dacă să presupunem că aceste numere au fost ghicite în primele patru ture, apoi putem spune că numărul de permutări a 4 elemente, care este 4x3x2x1 = 24, corespunde unei secvențe complete de combinări ale numerelor „norocoase” și deci reprezintă de fapt o singură variantă.

În cele din urmă, numărul combinărilor va fi:
 
 
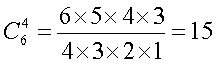
Această formulă pentru numărul de combinări este valabilă și pentru oricare alt număr de cifre hașurate și cifre ghicite. În general, se poate formula următoarea regulă: Pentru a determina numărul de variante cu m numere ghicite pentru n numere marcate este necesar să se calculeze numărul de combinări:
 
 
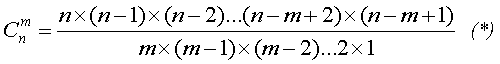
În această formulă, numărul de factori din numărător și numitor este același și este egal cu m.

Tot cu această formulă se calculează numărul total de combinații posibile pentru jocurile loto. Iar pentru Loto 6 din 49 obținem:
 
 
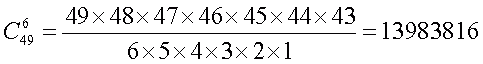
Pe baza la formula (*) și a calculelor specifice se completează tabelul cu numărul de câștiguri pentru fiecare categorie de câștig, în dependență de câte numere s-au marcat și câte numere au fost ghicite. Vezi ca exemplu tabelul pentru Loto 6/49.
 

 

Câștigul mediu al unei variante

Să trecem acum la estimarea câștigurilor care se calculează în funcție de câștigul mediu a unei variante jucate pentru fiecare categorie de câștig. Câștigul mediu reprezintă probabilitatea de apariție a acestui câștig înmulțită la suma totală de bani oferită pentru categoria de câștig respectivă.

Conform calculelor matematice rezultă, că valorile medii de câștig pentru fiecare leu cheltuit în sistemul simplu de joc și în sistemul desfășurat de joc, indiferent de câte numere s-au marcat, sunt aceleași. Dar totuși diferență între aceste două sisteme de joc există.

Dacă se ia o caracteristică statistică pentru un număr mare de jucători participanți, se observă că, cu creșterea numărului total de cifre marcate pe un bilet, câștigurile devin mai mari însă probabilitatea câștigurilor mici se micșorează brusc. De aici tragem concluzia, că dacă se joacă pentru sume mari atunci mai preferabil ar fi sistemul desfășurat de joc, iar dacă se acceptă câștiguri de categorii mai mici, fără a risca prea mult, atunci mai potrivit ar fi sistemul simplu.
 

Probabilitatea nereușitelor succesive

Care este probabilitatea a unei serii lungi de nereușite dacă pentru toate tragerile succesive alegem aceeași combinație de numere? Formula de mai jos, care se numește formula lui Bernoulli, ne permite să găsim probabilitatea, că participând la n extrageri, numărul de extrageri care nu vor avea nici un câștig va fi egal cu m:
 
 
unde q este probabilitatea pentru o extragere, că nu au fost ghicite 6 numere, 5 numere și 4 numere și care poate fi exprimată prin formula de mai jos:
 
 
unde , și sunt probabilitățile de ghicire a 6, 5 și 4 numere pentru o combinație simplă.

Pentru exemplu, pe baza formulei lui Bernoulli și a unor date inițiale statistice s-au obținut următoarele rezultate ale probabilităților de nereușită, pentru 4 extrageri:

1) Nu a fost nici un câștig: m = 4, P = 0,02 (2%)

2) A fost doar un câștig: m = 3, P = 0,13 (13%)

3) Au fost 2 câștiguri: m = 2, P = 0,33 (33%)

4) Au fost 3 câștiguri: m = 1, P = 0,37 (37%)

5) Toate extragerile au fost cu câștig: m = 0, P = 0,15 (15%)

2% + 13% + 33% + 37% + 15% = 100%

După cum vedem, probabilitatea de nereușite succesive cu aceeași combinație de numere scade odată cu creșterea numărului de participări, însă apariția câștigului nu garantează că el va fi unul mare.

În pofida faptului ca imprevizibilitatea este caracteristica de bază a jocului de noroc, am putea oare totuși alege o strategie care să fie cea mai optimală? Unicul sfat în acest sens ar fi alegerea rațională a unui anumit sistem de joc și aplicarea lui într-un mod succesiv.